![]()
"Jag vill inte ha
ett sånt där digitalt mirakel
som mäter ut min tidskonsumtion
jag vill behålla
mitt globala orakel
som ger mig kvar min odödlighetsillusion"
Göran Ekstrof
Tid är ett märkligt begrepp. Hos oss är det viktigt. Vi mäter tid, och vi jagar
tid. Vi stämmer möte, vi blir irriterade på SJ, vi jagar oss själva och varandra med
väckarklockor, stämpelklockor och alltmer avancerade bordsalmanackor. Detta mönster är
speciellt för vår del av världen och för vår tid. I österlandet är tid ointressant
eller nästan ointressant - bara det tidsbegrepp, som behövs för odlingar, dvs
väsentligen årstidsbegreppet, är viktigt.
Fysiker är ibland vårdslösa med tiden. Man mäter med extremt hög precision, men
man är för det mesta ointresserad av tidens "riktning". Man arbetar ofta med
reversibla processer, dvs med processer där klockan lika gärna kan gå baklänges som
framlänges. Det enda fysikaliska begrepp, som gör tidsaxelns riktning viktig, är entropin.
Entropin undergår med tiden en ödesbunden utveckling - då tiden går kan entropin
bara öka eller förbli konstant. Det förefaller därför som om universum går mot en
värmedöd.
Tidsbegreppet och tidsenheterna har fått stringens från två skilda håll - från
astronomiska observationer och från atomära mätningar.
Den astronomiska tidens noggrannhet är fullt tillräcklig i vardagssituationer. Men
hjälp av atomuren har vi emellertid fått möjlighet att mäta och definiera tid med
långt större precision.
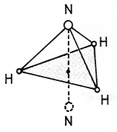 Schematisk bild av |
En av de första atomklockorna var den s k ammoniakklockan, som tillkom ungefär 1945.
NH3-molekylen är uppbyggd som en pyramid, där tre väteatomer bildar en
liksidig triangel. Om molekylen tillförs strålning med frekvensen 24 GHz börjar
kväveatomen att oscillera genom det plan, som definieras av de tre väteatomerna. Om
denna oscillation får stabilisera en sändare får vi en signal med en mycket
väldefinierad frekvens (relativ onoggrannhet 10-9).
Ett ännu bättre atomur är cesium-klockan. I denna utnyttjar man frekvensen för
övergången mellan två nivåer hos atomen cesium 133. Övergången induceras med ett
radiofrekvent fält. Då radiofrekvensen exakt motsvarar energin för övergången plockar
man ut signalen. Relativa onoggrannheten är 10-11 1967 ersattes den
astronomiska tiden med Cs-sekunden, och en sekund blev varaktigheten av 9 192 631 770
perioder av den strålning som motsvarar den nämnda övergången i cesium.
Exempel: Galileis längd- och tidmätningar
Idag är tidmätningar noggrannare än längdmätningar. Så har det inte alltid varit. För t ex Galilei var det enklare att mäta längd än att mäta tid. Hans tidmätare (vatten" klockor", dvs vattenspannar eller vattenrör med hål i botten) hade dålig precision. Nutida vetenskapsmän har betvivlat att Galilei utförde t ex det omtalade experimentet, där kulor rullade i rännor, och där sambandet mellan utgångshöjden och sluthastigheten kunde fastställas.
Nu har emellertid Vatikanens arkiv blivit tillgängligt, och 1973 publicerade professor Stillman Drake ett dittills okänt Galileimanuskript med teckningar och mätvärden. Dessa visade att Galilei kunde undvika tidmätning genom att i stället mäta hur långt från rännans kant, som kulan slog i underlaget. Fyrdubblas kulans utgångshöjd H, kommer kastvidden D att fördubblas. Galilei definierade alltså tid med hjälp av sträcka. Vi definierar sträcka med hjälp av tid.
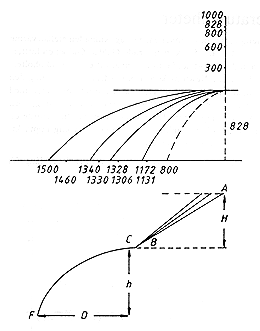
Överst syns Galileis ritning och siffervärden enligt det nyfunna manuskriptet.
De övre var de experimentella, de nedre de beräknade om hans fall-lag stämde. I den
nedre figuren visas hur man enkelt kan göra en efterkonstruktion av Galileis ränna. En
rullbana (av t ex en gardinstång) och en kula kan utnyttjas för att visa sambandet
mellan utgångshöjd och kastvidd.
Hemsida | Sök på servern | E-post till Webmistress | Personal och adresser