Ingen genomför ett experiment utan att ha en fråga, som han/hon söker svar på. Det
händer, att frågan är felställd. Det händer, att naturen svarar på något annat. Men
det finns alltid en fråga. Endast i eftergeneraliseringarnas värld kan man glömma bort
ursprungsfrågan och beskriva kunskapsgången som om man först gjort mätningar,
därefter ritat intressanta diagram och hittat samband. Så går det inte till.
Experimentet finns redan från början i ett sammanhang.
Låt oss se på ett exempel: mätning av ljusets hastighet. Det kom inte ett batteri av
frågor på en gång. Det började med spekulationer om att ljushastigheten kanske
var oändligt stor. På 1600-talet började man undra över om ljushastigheten var ändlig
eller oändlig, och det är knappast en slump att det var experimentalfysikens fader
Galilei som föreslog ett experiment, som skulle ge svar på frågan "ändlig eller
oändlig?".
Experimentet skulle innebära att två personer, A och B, hade var sitt ljus och var
sin skärm framför ljuset, så att de inte kunde se varandras ljus. A började med att ta
bort sin skärm och starta sin "klocka". Då B fick se A:s ljus, tog B bort sin
skärm. Då sedan A såg B:s ljus, stoppade A "klockan". Dubbla sträckan mellan
A och B dividerat med tiden skulle ge ett värde på ljushastigheten, om den var ändlig.
Var den oändlig, skulle tiden bli noll. - Se det gärna som ett utslag av Galileis
experimentella talang att han bara föreslog experimentet men aldrig genomförde det.
Det blev i stället dansken Ole Römer som fick svara på frågan om ljushastigheten
var ändlig. 1676 studerade han hur länge Jupiters måne Io* såg ut att vara i skugga
bakom Jupiter, dels då jorden var på väg från dels på väg mot Jupiter.
En eventuell tidsskillnad skulle visa att ljushastigheten var ändlig. De direkta
resultaten gav ett tveksamt "kanske" som svar på frågan om ljushastighetens
ändlighet. Men då Römer adderade tiderna för ett antal observationer av respektive
sort, blev svaret entydigt. Det fanns en tidsskillnad och ljusets hastighet var
ändlig!
* I Astronomy & Astrophysics Supplement Series 63, s 143, 1986 finns
en översiktsartikel om mätningar på Jupiters månar under perioden 1652 - 1983! Om
Ole Römers mätningar står: "Those observations are in this collection and they are
remarkably accurate and are quite valuable."
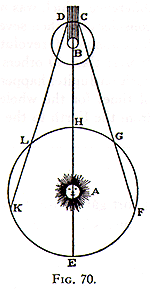
Let A (Fig. 70) represent the sun, B, Jupiter, C, the first Satellite as it enters Jupiter's shadow, to come out again at D, and let EFGHLK represent the Earth at different distances from Jupiter.
Now suppose that when the Earth is in L in the second quadrature of Jupiter, the first sateIIite has been viewed just at its emergence from the shadow at D; and that about 42 and one half hours Iater, that is after one revolution of this satellite, the Earth then being at K, it is seen again as it returns to D. It is then cIear that if light requires time to traverse the distance LK, the satellite will seem to return to D later than it wouId have if the Earth had remained at L, so that the revolution of this satellite, determined thus by its emergences, wiII be made longer by as much time as light would take to pass from L to K, and that on the contrary in the other quadrature FG, in which the Earth is approaching or going toward the light, the revolutions determined by the immersions will appear diminished by as much as those determined from the emergences appeared increased.
Ur Römers presentation inför Franska akademin
Han resonerar alltså om att en tidsskillnad skulle kunna observeras. Han förväntar
sig att denna skulle kunna bli ganska stor: om ljuset behövde en sekund för att
tillryggalägga en jorddiameter, skulle bandelarna FG respektive LK vardera ta 3,5
minuter, och tidsskillnaden mellan observationerna skulle vara hela 7 minuter. Så stor
var i varje fall inte tidsskillnaden. Men - fortsätter Römer:
It does not, however, follow that light needs no time; for after having examined the matter more closely he has found that this difference, which was not sensible in two revolutions, became very considerable when several of them were taken together, and that, for example, 40 revolutions observed from the side F were sensibly shorter than 40 others observed from the other side, in whatever position Jupiter happened to be, and this in the ratio of 22 (minutes of time) for the whoIe distance HE, which is twice the distance from the Earth to the Sun.
Ur Römers presentation inför Franska akademin
Hur fort går då ljuset? Från 1676 och fram till 1800-talets slut mätte man ljusets
hastighet med en successivt förbättrad precision. Först var man - liksom Römer -
hänvisad till kosmiska avstånd för att få noggranna värden. Vid mitten av 1800-talet
lyckades fransmannen Hippolyte Louis Fizeau bestämma ljusets hastighet genom mätningar
utförda på jorden. Han använde ett roterande kugghjul och skickade ljus mellan två
kuggar bort mot en avlägsen spegel (c:a 1 mil bort). Vid en viss rotationshastighet kunde
inte ljuset komma tillbaka genom kugghjulet - närmast intilliggande kugge var i vägen.
Vid ytterligare ökad rotationshastighet kunde ljuset passera igenom (i nästa
kuggmellanrum).
Fizeau genomförde ett liknande experiment tillsammans med sin landsman Jean Léon
Foucault. I det experimentet använde man en roterande spegel i stället för ett
roterande kugghjul. Experimentet var svårt och resultatet värt all beundran. Idag kan
man enkelt demon- strera metoden. Ljus reflekteras mot en roterande spegel och får sedan
färdas en lång väg innan det åter reflekteras mot den roterande spegeln.
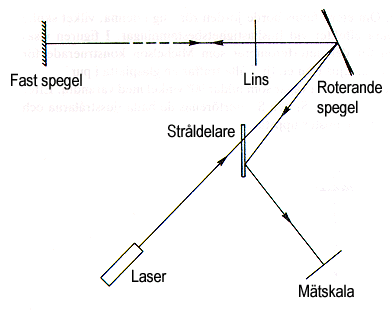
Mellan den roterande och den fasta spegeln är avståndet L. Ljuset passerar fram
och tillbaka (sträckan 2L), på tiden t=2L/c. Då har spegeln vridit sig varför reflexen
på mätskalan har flyttat sig. Med kännedom om storleken på denna förflyttning,
rotationsvarvtal och sträckan L kan ljushastigheten (c) beräknas.
Spegeln har under tiden vridit sig en viss vinkel. På en mätskala kan man se en
ljusfläck, vars läge kan bestämmas för olika rotationshastigheter. Ur mätresultaten
kan ljushastigheten beräknas.
Mot slutet av 1800-talet började frågeställningen byta karaktär. Man hade
övertygande kunnat visa att ljushastigheten i luft var ändlig och c:a 3,0 þ · 108
m/s. Man fortsatte att mäta med allt större noggrannhet, men frågan "hur fort går
ljuset?" började få konkurrens av frågan "vad är det, som bär fram
ljuset?" Man visste, att ljudvågor behöver något att utbreda sig i. Man trodde att
det samma gällde för ljuset. Detta okända något kallades för eter.*
* "eter" kommer från grekiskans "aether", vilket
betydde den himmelska luften, luften över månen. Luften under månen, den vanliga
luften, hette "aer" och antogs vara något annat.
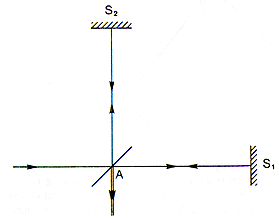Ett av de mest berömda
experimenten inom fysiken utfördes år 1881 av amerikanerna Albert Abraham Michelson och
Edward William Morley. Upphovet till experimentet var diskussionen om eterns existens. Om
etern fanns borde jorden röra sig i denna, vilket skulle ge mätbara effekter vid
ljushastighetsbestämningar. I figuren visas principen för den interferometer som
Michelson konstruerade för mätningarna. Ljus från en ljuskälla träffar en glasplatta
i punkten A. Ljuset delas upp i två vägar som bildar 90º vinkel med varandra. Efter
reflexion i speglarna S1 och S2 återförenas de båda
ljusstrålarna och ett interferensmönster uppstår.
Gångtiden fram och tillbaka mot S1 respektive S2 skulle bli
olika och bero på jordens hastighet i etern. Skillnaden i gångtid skulle ge ett
förskjutet interferensmönster. Man kan göra en jämförelse med två simmare, som kan
simma precis lika fort och som skall tillryggalägga samma sträcka. Den ene skall simma
längs med floden: först medströms till S1, sedan motströms tillbaka till A.
Den andre som skall simma tvärs över floden får flodens strömning från sidan, både
när han simmar mot S2 och när han simmar tillbaka till A. Det går lätt att
visa, att det skulle ta olika lång tid för de båda simmarna trots att de simmar lika
bra och skall lika långt.
Tog då även ljuset olika lång tid för att gå fram och tillbaka via S1
respektive S2? Fanns det någon eter, vars hastighet ljuset kunde få hjälp av
alternativt hindras av? Michelson och Morley mätte vid olika tider på dygnet och vid
olika årstider. Resultatet var entydigt. Man kunde aldrig se någon skillnad i
interferensmönstret. Vad det än var som bar fram ljuset, verkade det alltså inte som om
det kunde påverka utgången av Michelson - Morleys experiment.
Albert Einstein lade 1905 fram den speciella relativitetsteorin. Enligt denna finns
ingen "eter". Frågan vad det var som bar fram ljuset slutade dock inte att
ställas bara för att Einstein publicerade sin teori. Många, bl a Michelson, ansåg det
orimligt att etern inte skulle finnas. Mätningar för att påvisa etern pågick långt in
på 1920-talet innan alla hade accepterat den av teori och experiment stödda
uppfattningen att etern inte existerar och att ljus kan utbreda sig i vakuum.
Då var det dags att återvända till frågan "hur snabbt rör sig ljuset?"
1972 hade man nått fram till värdet
(2,9979245740,000000011) · 108 m/s.
Mätningen utfördes inte längre med dåliga ljuskällor, månrörelser eller
roterande kugghjul utan med allt mer förfinade interferometriska mätmetoder och med
lasrar. Mätningen 1972 utfördes med en infraröd laser. Några år senare gjorde man om
mätningen i det synliga området. Man mätte med bättre precision än den metern var
definierad med. Med en bättre meterdefinition hade man kunnat göra ännu noggrannare
ljushastighetsbestämningar. Det var en bakvänd situation, och 1983 vidtog man den enda
raka åtgärden: man definierade ljusets hastighet till 299792458 m/s och definierade
metern som den sträcka, som ljuset går i vakuum, på (1/299792458) s. Att man inte
definierade ljushastigheten och metern utifrån talvärdet 3 · 108 i stället
för 299792458, när metern nu ändå skulle definieras om, berodde på de
följdverkningar detta skulle fått för t ex densitetsvärden och för andra konstanter,
bla dielektricitetskonstanten för vakuum (jfr avsnittet Enheter).
Därmed har vi följt frågeställningarna kring ljusets hastighet från experimentens
början till deras definitiva slut. "Ändligt fort?" efterträddes av "Hur
fort?", vilket ersattes av "Vad bär fram ljuset?", vilket återgick till
"Hur fort?" vilket slutade med en förbättrad meterdefinition och att
frågan "Hur fort?" blev meningslös.
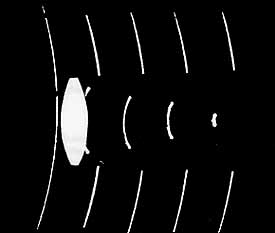
Foto: Nils Abramson
Numera kan man göra extremt korta ljuspulser. De ovanstående pulsfronterna
från en argonlaser är 10 pikosekunder (10 · 10-12 s) långa, dvs de har en
utsträckning på 3 · 108 · 10 · 10-12 m=3 mm! Pulsfronten kommer
in från vänster, träffar en lins och bryts samman till en punkt. En bild av linsen är
inklippt efteråt för att tydliggöra skeendet. I övrigt är det hela ett foto
(egentligen ett tredimensionellt sådant, ett hologram). Man kan alltså se att ljusets
hastighet är 3x108 m/s genom att notera att bredden på pulsfronterna är 3 mm
och att laserns pulser är 10 pikosekunder.
Den ljushastighetsbestämning som på 1600-talet krävde kosmiska avstånd kan nu
göras av ett människoöga, som tittar på en bild!
Metoden är uppfunnen av Nils Abramson, KTH.
 |
 |
 |
Hemsida | Sök på servern | E-post till Webmistress | Personal och adresser