Bodil Jönsson, Nina Reistad

Experiment, modell och teori

I den naturvetenskapliga kunskapsutvecklingen samverkar och konkurrerar den experimentella metoden med två andra metoder: att bilda modeller och att utforma teorier. I modell- och teoriutvecklingen hämtas ibland (men inte alltid) inspiration från observation av händelser. Modeller kan vara abstraherade ur verkligheten. Men teorier är inte härledda ur observationer - de är uppfunna för att förklara dem. Teorier kan därför aldrig bli bekräftade av experimentella resultat; de kan bara stödjas av experiment. Å andra sidan kan experimentella resultat helt kullkasta teorier. Teorier skall nämligen vara falsifierbara. *

* falsifierbara teorier går att undersöka och eventuellt kullkasta.

Medan experiment kan medverka till modellers och teoriers uppgång och fall, gäller också det omvända. Meningsfulla experiment föregås av en hypotes, en teoriansats. Nedan beskrivs födslovåndorna för två naturvetenskapliga begrepp: tryck respektive temperatur. Dessa båda begrepp fick inte stringens förrän man kunde göra experiment, men experimenten var möjliga först då man var i närheten av en (falsifierbar) teori.

Övergången mellan experiment och modell respektive modell och teori är ofta flytande. Eftersom denna boks tyngdpunkt ligger på experimentell fysik och inte på vetenskapsteori, tar vi här bara upp modell- och teoribildning i dess anknytning till experimentell verksamhet.

Modeller utmärks av att de är abstraktioner* av en verklighet, existerande eller tänkt. Vissa är åskådliga (t ex stadsplaneförslag och tryck-volym-temperaturytor för ideala gaser). Andra är abstrakta (t ex matematiska modeller). Modeller kan ibland uppstå direkt ur mätningar. Den ideala gasmodellen

pV = nRT

byggde exempelvis ursprungligen på mätningar. Förfinade mätresultat visade att sambandet bara var en approximation. Men det är fortfarande giltigt för modellen (abstraktionen) "ideal gas". Denna modell kännetecknas av anspråkslösa molekyler utan krav på vare sig eget utrymme eller kontakt sinsemellan. Modellens relevans förstärks av den kinetiska gasteorin, som ger en teoretisk förklaring till modellens funktion.

* abstrahera=dra ut ur.

Tankeexperiment är en annan metod, som samtidigt inrymmer både vissa av experimentets och modellens fördelar. Man behöver varken bekymra sig om tid, pengar eller experimentell genomförbarhet - man behöver bara tänka. Några av den moderna fysikens föregångsmän, bland dem Albert Einstein och Werner Heisenberg, byggde teorier på tankeexperiment.

Teorier och matematiska modeller flyter ibland samman. Betrakta t ex figuren nedan. Det är knappast meningsfyllt att diskutera huruvida påståendet i bildtexten görs utifrån teorin om gravitation eller utifrån den matematiska modellen att kraften är proportionell mot massan och omvänt proportionell mot kvadraten på avståndet.

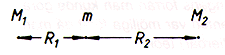
Meteoren m avlänkas åt vänster om M₁/R₁² är större än M₂/R₂².

Allmänt finns det emellertid en skillnad mellan matematisk modell och teori. Detta framgår bäst om man tar exempel från ett område, där teoribildning saknas. Betrakta figuren nedan. Den beskriver människors handelsvanor. Genom systematiska observationer har man konstaterat att benägenheten att handla i en viss stad beror på stadens storlek S och dess avstånd R från konsumenten. Personen P:s köpiust är närmare bestämt proportionell mot S/R²

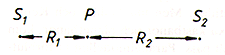
Personen P handlar i staden S₁ om S₁/R₁² är större än S₂/R₂².

Det finns dock ingen teori bakom sambandet - det är en tolkning av mätvärden varför modellen troligen inte gäller under alla omständigheter, Men den kan gälla som en matematisk modell under givna premisser.

Teorier och experiment lever ofta sina egna liv, oberoende av varandra. Modeller kan ibland tjäna som ett övergångsmedium mellan två egentligen oförenliga världar, exempelvis den rena matematikens respektive naturens. Modeller och teorier är generellt varken sanna eller falska, de är bara mer eller mindre användbara i olika områden.

Låt oss betrakta några exempel.

Exempel: Gauss formel

Gauss formel

är ett rent matematiskt samband mellan två variabler x och y ( och utgör parametrar). Sambandet är teoretiskt uppbyggt inom den rena, icke-empiriska matematiken. Det finns egentligen inga motiv till att denna teori skulle vara en bra beskrivning av statistiken i en mätserie enligt

där <x> är medelvärdet och s standardavvikelsen. Mätvärdenas normalfördelning utgör en framgångsrik modell (en bland många möjliga). Gauss formel är däremot rent teoretisk.

Exempel: Kägelsnitt, planetbanor och bollkastning

De gamla grekerna var mycket förtjusta i kägelsnitt. Deras kunskaper om ellipser, parabler och hyperbler var kanske inte så praktiskt värdefulla för samtiden. Men när Galilei och Kepler tvåtusen år senare skulle tolka kastbanor och planetbanor, kom kägelsnittsformalismen väl till pass. Parabelmodellen är förbluffande bra för att beskriva kastbanor. Ellipsmodellen är förbluffande bra för att beskriva planetbanor. Om man funderar närmare över detta, blir man bara mer och mer förbryllad. Snitt genom några käglor ger några geometriska former, som sedan återfinns hos rörelser i kosmos?!

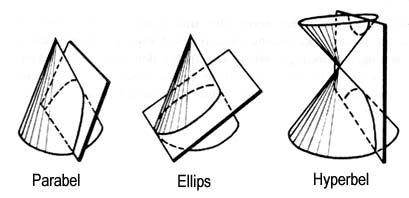
Kurvtyper som erhålls genom att skära koner med plan.

Hemsida | Sök på servern | E-post till Webmistress | Personal och adresser